图
图中的最长环
前言:关于图的性质
「每个节点至多有一条出边」意味着,对于图中任意一个大小为 m 的连通块,有 m 个点,每个点至多出去一条边,所以连通块至多有 m 条边。
我们知道,m 个点 m−1 条边的连通图是一棵树,在树上增加一条有向边,至多会形成一个环。(这样的图叫做内向基环树)
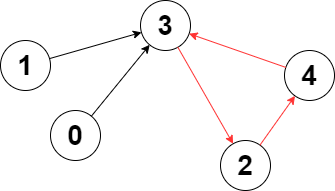
假设你在跑步,操场跑道是 3→2→4→3(上图红线)。
你想知道跑一圈要多久。你从节点 0 开始跑,跑到节点 3 的时候,记录当前时间为 t 1=2,再次跑到节点 3 的时候,记录当前时间为 t 2=5,那么跑一圈就需要 t 2−t 1=5−2=3 个单位时间。如果每访问一个节点,计时器就加一,那么 t 2−t 1就是跑道长度,即环长
初始时间为 curTime=1。遍历图,每访问到一个新的节点 x,就记录首次访问时间 visTime[x]=curTime,然后将 curTime 加一。
假设我们从节点 i 开始。首先记录开始时间 startTime=curTime,然后继续走**,如果走到死路,或者找到了一个之前访问过的点 x,则退出循环**。
退出循环后,分类讨论:
- 如果 visTime[x]<startTime,说明** x 不是在本轮循环中访问的**。因为x的访问时间早于startTime,在上几轮就已经访问过了,例如上图从节点 0 开始,访问节点 0,3,2,4。然后接着从节点 1 开始,访问节点 3,发现 visTime[3] 比访问节点 1 的时间还要早,那么包含节点 3 的环长我们之前已经计算过了,无需再次计算。
- 如果 visTime[x]≥startTime,说明 x 是在本轮循环中访问的,且被访问了两次。这只有一种可能,就是 x 在环上。根据前后两次访问 x 的时间差,就能算出环长,即 curTime−visTime[x]。
java
class Solution {
public int longestCycle(int[] edges) {
int res = -1;
int len = edges.length;
int[] firstTime = new int[len];
int start = 0;
int cur = 1;
for(int i = 0; i< len; i++){
start = cur;
int j = i;
while(edges[j] != -1 && firstTime[j] == 0){
firstTime[j] = cur;
cur++;
j = edges[j];
}
if(edges[j] != -1 && firstTime[j] >= start){
res = Integer.max(res,cur - firstTime[j]);
}
}
return res;
}
}